teoremin tanımı
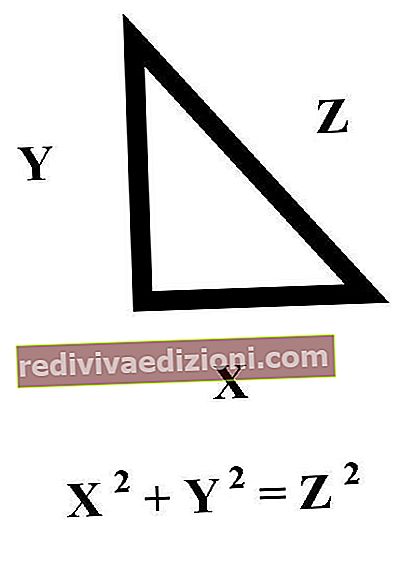Teoremler matematiğin ihtiyacı ve özel ilgisidir ve onlar hakkında konuşurken, mantıksal bir çerçeve içinde doğru olduğu kanıtlanabilecek ifadelere atıfta bulunulur .
Genel olarak, teoremler, cevap olarak adlandırıldıkları önceden numaralandırılabilen veya tahmin edilebilen bir dizi koşuldan oluşur . Bunların ardından, söz konusu çalışmanın koşullarında, yani her şeyden önce teoremin bilgilendirici içeriğinde açıkça her zaman doğru olacak olan sonuç veya matematiksel ifade ortaya çıkacaktır. hipotez ve tez veya çalışmanın tamamlanması.
Ancak, belirli bir ifade bir teorem haline gelmek için makul olduğunda matematik için kaçınılmaz olan bir şey vardır ve bu, matematik topluluğu içinde ve matematik topluluğu için yeterince ilginç olmalıdır, aksi takdirde ve ne yazık ki, basitçe bir slogan, bir sonuç veya sadece bir önerme olabilir asla bir teorem olamamak.
Ve konuyu biraz daha açıklığa kavuşturmak için, yukarıda bahsettiğimiz kavramları da ayırt etmek gerekir, böylece matematiksel bir topluluğun parçası olmasak bile, bunun bir teorem, bir lemma olduğunu anlayabiliriz. bir sonuç veya bir öneri.
Bir Lemma bir önermedir, evet, ancak daha uzun bir teoremin parçasıdır. Sonuç, bir teoremi izleyen bir ifadedir ve son olarak önerme, herhangi bir belirli teoremle ilişkili olmayan bir sonuçtur.
Başlangıçta bir teoremin yalnızca mantıksal bir çerçeve içinde kanıtlanabilen bir ifade olduğunu belirttik, mantıksal bir çerçeve ile bir dizi aksiyom veya aksiyomatik sisteme ve teoremleri türetmemize izin verecek bir çıkarım sürecine atıfta bulunuyoruz. Daha önce türetilmiş aksiyomlar ve teoremler.
Öte yandan, iyi biçimlendirilmiş mantıksal formüllerin sonlu dizisi bu teoremin bir kanıtı olarak adlandırılacaktır.
Matematiğin teoremlere verdiği özel ilgi olmasa da, fizik veya ekonomi gibi disiplinler genellikle diğerlerinden çıkarılan ve teorem olarak da adlandırılan ifadeler üretir.
